A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

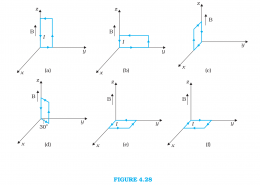
Magnetic field strength, B = 3000 G = 3000 x 10^-4 T = 0.3 T

Length of the rectangular loop, l=10 cm

Width of the rectangular loop, b = 5 cm

Area of the loop, A = l x b = 10×5 = 50 cm² = 50 x 10⁻⁴m²

Current in the loop, I = 12 A

Now, taking the anti-clockwise direction of the current as positive and vice-versa:

Ans (a).

Torque, τ= IA x B   (τ,A & B in vector forms)

From the given figure, it can be observed that A is normal to the y-z plane and B is directed along the z-axis.

Therefore,

τ = 12 x (50 x 10⁻⁴ ) i x 0.3k  (i ,j & k in vector forms)

= -1.8×10⁻²j Nm

The torque is 1.8×10² N m along the negative y-direction. The force on the loop is zero because the angle between A and B is zero.

Ans (b).

This case is similar to case (a). Hence, the answer is the same as (a).

Ans (c).

Torque,  τ= IAxB            (τ,A & B in vector forms)

From the given figure, it can be observed that A is normal to the x-z plane and B is directed along the z-axis.

Therefore ,

τ= -12 x (50 x 10⁻⁴ ) i x 0.3k  (i ,j & k are vectors)

= —1.8×10^-2 i Nm

The torque is 1.8×10^-2 Nm along the negative x direction and the force is zero.

Ans (d).

Magnitude of torque is given as:

|τ| = IAB

= 12x50x10⁻⁴x0.3 = 1.8×10⁻²Nm

The torque is 1.8×10⁻² N m at an angle of 240° with positive x direction. The force is zero.

Ans (e).

Torque, τ = IAxB = (50×10⁻⁴ x 12) k x 0.3k = 0          (τ,A & B in vector forms) and (i ,j & k are vectors)

Hence, the torque is zero. The force is also zero.

Ans (f).

Torque τ = IAxB            (τ,A & B in vector forms) and (i ,j & k are vectors)

= (50×10⁻⁴x 12 ) k x 0.3 k = 0

Hence, the torque is zero. The force is also zero.

In case (e), the direction of IA and B is the same and the angle between them is zero. If displaced, they come back to an equilibrium. Hence, its equilibrium is stable.

Whereas, in case (f), the direction of IA and B is opposite. The angle between them is 180°. If disturbed, it does not come back to its original position. Hence, its equilibrium is unstable.