100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:

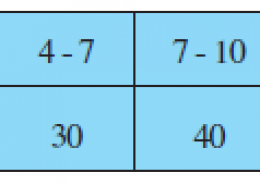
The cumulative frequency with their respective class intervals are as follows.

It can be observed that the cumulative frequency just greater than n/2 (i.e. 100/2 = 50) is 76, belonging to class interval 7 – 10.
Median class = 7-10
lower limit (l) of median class = 7
Cumulative frequency (cf) of class preceding median class = 36
Frequency (f) of median class = 40
Class size (h) = 3
Median = l + ((n/2 – cf)/f) × h = 7 + ((50 – 36)/40) × 3 = 7 + 42/40 = 7 + 1.05 = 8.05
To find the class marks of the given class intervals, the following relation is used.
xᵢ = (Upper limit + Lower limit)/ 2
Taking 11.5 as assumed mean (a), dᵢ, uᵢ, and fᵢuᵢ are calculated according to step deviation method as follows.
Number of letters 1-4 4-7 7-10 10-13 13- 16 16-19 Total
No. of surnames (fᵢ) 6 30 40 16 4 4 100
xᵢ 2.5 5.5 8.5 11.5 14.5 17.5
dᵢ = xᵢ – 11.5 -9 – 6 -3 0 3 6
uᵢ = dᵢ / 3 -3 2 1 0 1 2
fᵢuᵢ -18 -60 -40 0 4 8 -106
From the table, we obtain
∑fᵢ = 100, ∑fᵢuᵢ = -106, a = 11.5 and h = 3
mean (X̄) = a + (∑fᵢuᵢ / ∑fᵢ)h = 11.5 + (-106/100) × 3 = 11.5 – 318/100 = 11.5 – 3.18 = 8.32
The data in the given table can be written as
Number of Letters 1-4 4-7 7-10 10-13 13-16 16-19 Total (n)
Frequency (fᵢ) 6 30 40 16 4 4 100
From the table, it can be observed that the maximum class frequency is 40 belonging to class interval 7 – 10.
Modal class = 7 – 10
Lower limit (l) of modal class = 7
Class size (h) = 3
Frequency (f₁) of modal class = 40
Frequency (f₀) of class preceding the modal class = 30
Frequency (f₂) of class succeeding the modal class = 16
Mode = l + ((f₁ – f₀)/2f₁ – f₀ – f₂) × h = 7 + ((40 – 30) / 2 × 40 – 30 -16) × 3 = 7 + 10/34 × 3 = 7 + 0.88 = 7.88
Therefore, median number and mean number of letters in surnames is 8.05 and 8.32 respectively while modal size of surnames is 7.88.