Determine the median number of letters in the surnames. Find the mean number of letters in the surnames? Also, find the modal size of the surnames.
NCERT Class 10 Math’s Chapter 14
Page No. 289
Exercise 14.3
Question No. 6
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:
Share
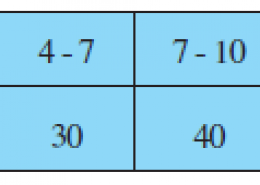
The cumulative frequency with their respective class intervals are as follows.
It can be observed that the cumulative frequency just greater than n/2 (i.e. 100/2 = 50) is 76, belonging to class interval 7 – 10.
Median class = 7-10
lower limit (l) of median class = 7
Cumulative frequency (cf) of class preceding median class = 36
Frequency (f) of median class = 40
Class size (h) = 3
Median = l + ((n/2 – cf)/f) × h = 7 + ((50 – 36)/40) × 3 = 7 + 42/40 = 7 + 1.05 = 8.05
To find the class marks of the given class intervals, the following relation is used.
xᵢ = (Upper limit + Lower limit)/ 2
Taking 11.5 as assumed mean (a), dᵢ, uᵢ, and fᵢuᵢ are calculated according to step deviation method as follows.
Number of letters 1-4 4-7 7-10 10-13 13- 16 16-19 Total
No. of surnames (fᵢ) 6 30 40 16 4 4 100
xᵢ 2.5 5.5 8.5 11.5 14.5 17.5
dᵢ = xᵢ – 11.5 -9 – 6 -3 0 3 6
uᵢ = dᵢ / 3 -3 2 1 0 1 2
fᵢuᵢ -18 -60 -40 0 4 8 -106
From the table, we obtain
∑fᵢ = 100, ∑fᵢuᵢ = -106, a = 11.5 and h = 3
mean (X̄) = a + (∑fᵢuᵢ / ∑fᵢ)h = 11.5 + (-106/100) × 3 = 11.5 – 318/100 = 11.5 – 3.18 = 8.32
The data in the given table can be written as
Number of Letters 1-4 4-7 7-10 10-13 13-16 16-19 Total (n)
Frequency (fᵢ) 6 30 40 16 4 4 100
From the table, it can be observed that the maximum class frequency is 40 belonging to class interval 7 – 10.
Modal class = 7 – 10
Lower limit (l) of modal class = 7
Class size (h) = 3
Frequency (f₁) of modal class = 40
Frequency (f₀) of class preceding the modal class = 30
Frequency (f₂) of class succeeding the modal class = 16
Mode = l + ((f₁ – f₀)/2f₁ – f₀ – f₂) × h = 7 + ((40 – 30) / 2 × 40 – 30 -16) × 3 = 7 + 10/34 × 3 = 7 + 0.88 = 7.88
Therefore, median number and mean number of letters in surnames is 8.05 and 8.32 respectively while modal size of surnames is 7.88.