Find the median length of the leaves.
(Hint: The data needs to be converted to continuous classes for finding the median, since the formula assumes continuous classes. The classes then change to 117.5 – 126.5, 126.5 – 135.5, . . ., 171.5 – 180.5.)
The lengths of 40 leaves of a plant are measured correct to the nearest millimetre, and the data obtained is represented in the following table :
Share
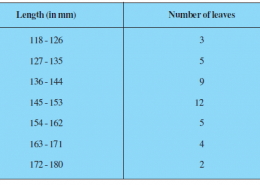
The given data does not have continuous class intervals. It can be observed that the difference between two class intervals is 1. Therefore, 1/2 = 0.5 has to be added and subtracted to upper class limits and lower-class limits respectively.
Continuous class intervals with respective cumulative frequencies he represented follows.
From the table, it can be observed that the cumulative frequency just greater than n/2 (i.e. 40/2 = 20) is 29, belonging to class interval 144.5 – 153.5.
Median class = 144.5 – 153.5
Lower Limit (l) of median class = 144.5 and class size (h) = 9
Frequency (f) of median class 12
Cumulative frequency (cf) of class preceding median class = 17
Median = l + (n/2 – cf)/f) × h = 144.5 + ((20 – 17)/12) × 9 = 144.5 + 2.25 = 146.75
Therefore, median length of leaves is 146.75mm.
See this explanation video for better understanding✌😃