In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Figure). Show that: (i) Δ AMC ≅ Δ BMD (ii) ∠ DBC is a right angle. (iii) Δ DBC ≅ Δ ACB (iv) CM = (1/2) AB

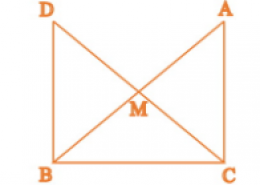
(i) In ΔAMC and ΔBMD,
CM = DN [∵ Given]
∠AMC = ∠BMD [∵ Vertically Opposite Angles]
AM = MB [∵ M is the mid-point of line segment AB]
Hance, ΔAMC ≅ ΔBMD [∵ SAS Congruency Rule]

(ii) ΔAMC ≅ ΔBMD [∵ Proved above]
∠CAM = ∠DMB [∵ Corresponding parts of congruent Triangles are equal ]
Since, alternate angles (∠CAM and ∠DMB) are equal, therefore AC ∥ BD.
∠ACB + ∠DBC = 180° [∵ Co-interior angles]
⇒ 90° + DBC = 180° [∵ Angle C is right angle]
⇒ ∠DBC = 180° – 90° = 90°
Hence, ∠DBC is a right angle.

(iii) In ΔDBC and ΔACB
DB = AC [∵ ΔAMC ≅ ΔBMD]
∠DBC = ∠ACB [∵ Proved above]
BC = BC [∵ M is the mid-point of line segment AB]
Hence, ΔDBC ≅ ΔACB [∵ SAS Congruency Rule]