Prove the angle-angle-side congruence criterion.
What is implies rhombus.
Quadrilaterals Solutions for Class 9th Maths.
9th Maths EXERCISE 8.1,Page No:146, Questions No:6, Session 2023-2024.
Class 9th, NCERT Books for Session 2023-2024, based on CBSE Board.
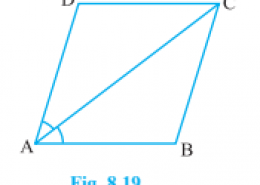
(i) ∠DAC = ∠BAC …(1) [∵ Given]
∠DAC = ∠BCA …(2) [∵ Alternate angle]
∠BAC = ∠ACD …(3) [∵Alternate angles]
From the equations (1), (2) and (3), we have
∠ACD = ∠BCA …(4)
Hence, Diagonal AC bisects angle C also.
(ii) From the equation (2) and (4), we have
∠ACD = ∠DAC
In ΔADC,
∠ACD = ∠DAC [∵ Prove above]
AD = DC [∵ In a triangle, the sides opposite to equal angle are equal]
A parallelogram whose adjacent sides are equal, is a rhombus. Hence, ABCD is a rhombus.
If the diagonal AC of a parallelogram ABCD bisects ∠A, then ∠DAC = ∠BAC. Using alternate interior angles (∠DAC = ∠BCA and ∠BAC = ∠DCA), it follows that ∠BCA = ∠DCA, so AC also bisects ∠C. Additionally, since ∠DAC = ∠BAC, then ∠DCA = ∠BCA, which means DA = DC, and because opposite sides of a parallelogram are equal, AB = BC = CD = DA, making ABCD a rhombus.
Step-by-step explanation:
Given: Parallelogram ABCD, and diagonal AC bisects ∠A. This means ∠DAC = ∠BAC.
Alternate Interior Angles:
Since AB is parallel to CD, with AC as a transversal, then ∠DAC = ∠BCA (alternate interior angles).
Since AD is parallel to BC, with AC as a transversal, then ∠BAC = ∠DCA (alternate interior angles).
Bisecting ∠C:
From the given condition, ∠DAC = ∠BAC.
From the alternate interior angles, we have ∠DAC = ∠BCA and ∠BAC = ∠DCA.
Therefore, by substitution, ∠DCA = ∠BCA.
This proves that AC bisects ∠C.
Proving it’s a Rhombus:
From step 3, we found ∠DCA = ∠BCA.
Also, we know ∠DCA = ∠BAC and ∠BCA = ∠DAC.
This means ∠DAC = ∠BAC = ∠BCA = ∠DCA.
Consider triangle ADC. Since ∠DAC = ∠DCA, the sides opposite to these equal angles are also equal, so DA = DC.
In a parallelogram, opposite sides are equal (DA = BC and AB = CD).
Therefore, AB = BC = CD = DA.
Thus, all sides of the parallelogram are equal, and ABCD is a rhombus.