A curved mirror, whether concave or convex, has a focal point where parallel rays either converge (concave) or diverge (convex). This point, called the focal point, is crucial in understanding image formation and optical properties of curved mirrors.
An object of height h is kept at point P in front of a mirror as shown below. The height of the image produced is h’. In the diagram, F is the focus and C is the centre of curvature. (a) If the object is now moved to point C, will the height of the image now produced be less than, equal to, or greater than h’? Give a reason for your answer. (b) If the focal length of the mirror is 20 cm and the distance between points P and C is 10 cm, determine the distance between the images produced when the object is kept at P and C.
Share
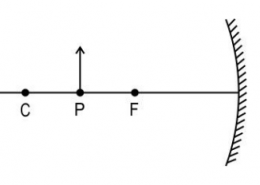
(a) The height of the image produced when the object is at C will be less than h’. The magnification is more when the object is at point P than at C.
(b) To find the distance between the two images we need to find the image distance when the object is at P and when it is at C.
To find the image distance when the object is at P:
u = -30 cm
f = -20 cm
Using mirror formula v1 = – 60 cm
To find the image distance when the object is at C:
Since C is the centre of curvature, image distance = object distance (i.e.) v2 = – 40 cm.
Distance between the images = |v2| – |v1| = 60 – 40 = 20 cm