What is the side-angle-side (SAS) congruence criterion.
Prove the corresponding parts of congruent triangles
Quadrilaterals Solutions for Class 9th Maths.
9th Maths EXERCISE 8.1,Page No:147, Questions No:12, Session 2023-2024.
ABCD is a trapezium in which AB || CD and AD = BC see Figure. Show that (i) ∠ A = ∠ B (ii) ∠ C = ∠ D (iii) ∆ ABC ≅ ∆ BAD (iv) diagonal AC = diagonal BD
Share
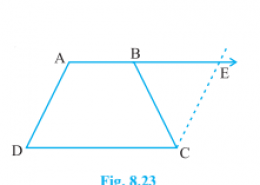
In AECD,
AE ∥ DC [∵ Given]
AD ∥ CE [∵ By construction]
Hence, AECD is a parallelogram.
AD = CE …(1) [∵ Opposite sides of a parallelogram are equal]
AD = BC …(2) [∵ Given]
Hence, CE = BC [∵ From the equation (1) and (2)]
Therefore, in ΔBCE,
∠3 = ∠4 …(3) [∵ In a triangle, the angles opposite to equal sides are equal]
Here, ∠2 + ∠3 = 180° …(4) [∵ Linear Pair]
∠1 + ∠4 = 180° …(5) [∵ Co-interior angles]
Therefore, ∠2 + ∠3 = ∠1 + ∠4 [∵ From the equation (4) and (5)]
⇒ ∠2 = ∠1 ⇒ ∠B = ∠A [∵ ∠3 = ∠4]
(ii) ABCD ia a trapezium in which AB ∥ DC, hence,
∠1 + ∠D = 180° …(6) [∵ Co-interior angles]
∠2 + ∠C = 180° …(7) [∵ Co-interior angles]
Therefore, ∠1 + ∠D = ∠2 + C [∵ From the equation (6) and (7)]
⇒ ∠D = ∠C [∵ ∠2 = ∠1]
(iii) In ΔABC and ΔBAD,
BC = AD [∵ Given]
∠ABC = ∠BAD [∵ Prove above]
AB = AB [∵ Common]
Hence, ΔABC ≅ ΔBAD [∵ SAS Congruency rule]
(iv) ΔABC ≅ ΔBAD [∵ Prove above]
Diagonal AC = diagonal BD [∵ CPCT]