A life insurance agent found the following data for distribution of ages of 100 policy holders.

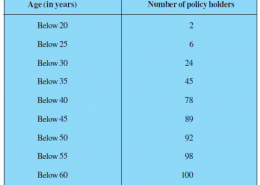
Here, class width is not the same. There is no requirement of adjusting the frequencies according to class intervals. The given frequency table is of less than type represented with upper class limits. The policies were given only to persons with age 18 years onwards but less than 60 years. Therefore, class intervals with their respective cumulative frequency can be defined as below.

From the table, it can be observed that n = 100
Cumulative frequency (cf) just greater than n/2 (i.e. 100/2 = 50) is 78, belonging to interval 35 – 40.
Therefore, median class = 35 – 40
Lower limit (l) of median class = 35
Frequency (f) of median class = 33
Cumulative frequency (cf) of class = 45
Frequency (f) of median class = 33
Median = l + ((n/2 – cf)/(f)) × h = 35 + {(50 – 45)/20} × 5 = 35 + 25/33 = 35 + 0.76 = 35.76
Therefore, median age is 35.76 years.

See here for Video explanation 👇😀