Prove by the Side-Side-Side (SSS) congruence criterion.
How to Substituting these equalities.
TRIANGLES Solutions for Class 9th Maths.
9th Maths EXERCISE 7.3,Page No:128, Questions No:1, Session 2023-2024.
Δ ABC and Δ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Figure). If AD is extended to intersect BC at P, show that (i) Δ ABD ≅ Δ ACD (ii) Δ ABP ≅ Δ ACP (iii) AP bisects ∠ A as well as ∠ D. (iv) AP is the perpendicular bisector of BC.
Share
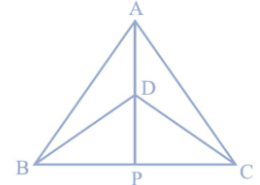
In ΔABD and ΔACD,
AB = AC [∵ Given]
BD = CD [∵ Given]
AD = AD [∵ Common]
Hence, ΔABD ≅ ΔACD [∵ SSS Congruency Rule]
(ii) In ΔABD ≅ ΔACD, [∵ Proved above]
∠BAD = ∠CAD [∵ CPCT]
In ΔABP and ΔACP,
AB = AC [∵ Given]
∠BAP = ∠CAP [∵ Proved above]
AP = AP [∵ Common]
Hence, ΔABP ≅ ΔACP [∵ SAS Congruency Rule]
(III) In ΔABD ≅ ΔACD [∵ Proved above]
∠BAD = ∠CAD [∵ CPCT]
∠BDA = ∠CDA [∵ CPCT]
Hence, AP bisects both the angles A and D.
(iv) In ΔABP ≅ ΔACP [∵ Proved above]
BP = CP [∵ CPCT]
∠BPA = ∠CPA [∵ CPCT]
∠BPA + ∠CPA = 180° [∵ Linear pair]
⇒∠CPA + ∠CPA = 180° [∵∠BPA = ∠CPA]
⇒ 2∠CPA = 180° ⇒∠CPA = (180°/2 = 90°
⇒ AP is perpendicular to BC. ⇒ AP is Perpendicular bisector of BC. [∵ BP = CP]