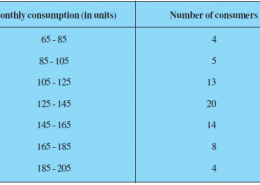
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality.

To find the class marks, the following relation is used.
xᵢ = (Upper limit + Lower limit)/2
Taking 135 as assumed mean (a). dᵢ, uᵢ, fᵢuᵢ are calculated according to step deviation method as follows.

From the table, we obtain.
∑fᵢ = 68, ∑fᵢuᵢ = 7, a = 135 and h = 20
mean (X̄) = a + (∑fᵢuᵢ / ∑fᵢ)h = 135 + (7/68) × 20 = 135 + 2.058 = 137.058
From the table, it can be observed that the maximum class frequency is 20, belonging to class interval 125 – 145.
Modal class 125 – 145
Lower limit (l) of modal class = 125
Class size (h) = 20
Frequency (f₁) of modal class = 20
Frequency (f₀) of class preceding modal class = 13
Frequency (f₂) of class succeeding the modal class = 14
Mode = l + (f₁ – f₀ / 2f₁ – f₀ – f₂)h = 125 × (20 – 13 / 2 × 20 – 13 – 14) × 20 = 125 + 7/13 × 20 = 125 + 10.76 = 135.76
To find the median of the given data, cumulative frequency is calculated as follows.
Monthly consumption (in units) Number of consumers Cumulative frequency
65 – 85 4 4
85 – 105 5 4 + 5 = 9
105 – 125 13 9 + 13 = 22
125 – 145 20 22 + 20 = 42
145 – 165 14 42 + 14 = 56
165 – 185 8 56 + 8 = 64
185 – 205 4 64 + 4 = 68
From the table, we obtain n = 18
Cumulative frequency (cf) just greater than n/2 (i.e, 68/2 = 34) is 42, belonging to interval 125 – 145.
Therefore, median class = 125 – 145
Lower limit (l) of median class = 125 and class size (h) = 20
Frequency (f) of median class = 20
Cumulative frequency (cf) of class preceding median class = 22
Median = l + ((n/2 – cf)/f) × h = 125 + (34 – 22 / 20) × 20 = 125 + 12 = 137
Therefore, median, mode, mean of the given data is 137, 135.76, and 137.05 respectively.
The three measures are approximately the same in this case.