Define the opposite angles of quadrilateral.
To prove the opposite angles of quadrilateral are supplementary.
Class 9th Maths Important Question Answer, Session 2023-2024.
Quadrilaterals, EXERCISE 8.1, Page No: 147, Questions No:11.
In ∆ ABC and ∆ DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig. 8.22). Show that (i) quadrilateral ABED is a parallelogram (ii) quadrilateral BEFC is a parallelogram (iii) AD || CF and AD = CF (iv) quadrilateral ACFD is a parallelogram (v) AC = DF (vi) ∆ ABC ≅ ∆ DEF.
Share
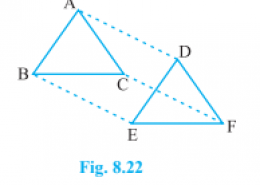
(i) In ABED, AB = DE [∵ Given]
AB ∥ DE [∵ Given]
Hence, ABED is a parallelogram.
(ii) In BEFC, BC = EF [∵ Given]
BC ∥ EF [∵ Given]
Hence, BEFC is a parallelogram.
(iii) In ABED,
AD = BE …(1) [∵ ABED is a parallelogram]
AD ∥ BE …(2) [∵ ABED is a parallelogram]
In BEFC,
BE = CF …(3) [∵ ABED is a parallelogram]
BE ∥ CF …(4) [∵ ABED is a parallelogram]
From (2) and (4), we have
AD ∥ CF …(5)
From (1) and (3), we have
AD = CF …(6)
(iv) In ACFD,
AD = CF [∵ From (6)]
AD ∥ CF [∵ From (5)]
Hence, ACFD is a parallelogram
(v) In ACFD,
AC = DF . [∵ ACFD is a parallelogram]
(vi) In ΔABC and ΔDEF
AB = DE [∵ Given]
AC = DF [∵ Proved above]
BC = EF [∵ Given]
Hence, ΔABC ≅ ΔDEF [∵ SSS Congruency rule]