Home/ Questions/Q 215553
Next
Answered
keshav kumar
  • 1
Asked: 2023-03-31T03:19:04+00:00 In:

In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ see Figure. Show that: (i) ∆ APD ≅ ∆ CQB (ii) AP = CQ (iii) ∆ AQB ≅∆ CPD (iv) AQ = CP (v) APCQ is a parallelogram

  • 1
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ see Figure. Show that: (i) ∆ APD ≅ ∆ CQB (ii) AP = CQ (iii) ∆ AQB ≅∆ CPD (iv) AQ = CP (v) APCQ is a parallelogram

Opposite angles in a parallelogram, why are congruent.
To prove is a diagonal of parallelogram.
Class 9th Maths, Page No:147, Questions No:9, Exercise 8.1
NCERT, Solutions for Class 9th Maths, Session 2023-2024.

class 9mathsncert
Share

    1 Answer

    1. Best Answer
      In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ see Figure. Show that: (i) ∆ APD ≅ ∆ CQB (ii) AP = CQ (iii) ∆ AQB ≅∆ CPD (iv) AQ = CP (v) APCQ is a parallelogram

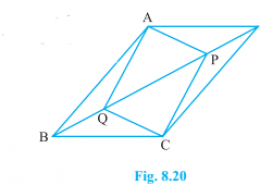
      (i) In ΔAPD and ΔCQB,
      DP = BQ [∵ Given]
      ∠ADP = ∠CBQ [∵ Alternate angle]
      AD = BC [∵ Opposite sides of a parallelogram]
      Hence, ΔAPD ≅ ΔCQB [∵ SAS Congruency rule]

      (ii) ΔAPD ≅ CQB [∵ Prove above]
      AP = CQ …(1) [∵ CPCT]

      (iii) In ΔAQB and ΔCPD,
      QB = DB [∵ Given]
      ∠ABQ = ∠CDP [∵ Alternate angle]
      AB = CD [∵ Opposite sides of a parallelogram]
      Hence, ΔAQB ≅ ΔCPD [ SAS Congruency rule]

      (iv) ΔAQB ≅ ΔCPD [∵ Prove above]
      AQ = CP …(2) [∵ CPCT]

      (v) In APCQ,
      AP = CQ [∵ From (1)]
      AQ = CP [∵ From (2)]
      The opposite sides of quadrilateral APCQ are equal.
      Hence, APCQ is a parallelogram.

      • 7
    Leave an answer

    Leave an answer

    Browse