Δ ABC and Δ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Figure). If AD is extended to intersect BC at P, show that (i) Δ ABD ≅ Δ ACD (ii) Δ ABP ≅ Δ ACP (iii) AP bisects ∠ A as well as ∠ D. (iv) AP is the perpendicular bisector of BC.

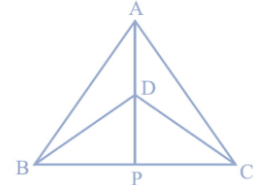
(i) In ΔABD and ΔACD
AB = AC [∵ Given]
BD = CD [∵ Given]
AD = AD [∵ Common]
Hence, ΔABD ≅ ΔACD [∵ SSS Congruency Rule]
(ii) In ΔABD ≅ ΔACD [∵ Proved above]
∠ BAD = ∠ CAD [∵ CPCT]
In ABP and ACP,
AB = AC [∵ Given]
∠ BAP = ∠ CAP [∵ Proved above]
AP = AP [∵ Common]
Hence, ΔABP ≅ ΔACP [∵ SAS Congruency rule]
(iii) In ΔABD ≅ ΔACD [∵ Proved above]
∠ BAD = ∠ CAD [∵ CPCT]
∠ BDA = ∠ CDA [∵ CPCT]
Hence, AP bisects both the angles A and D
(iv) In ΔABP ≅ ΔACP [∵ Prove above]
BP = CP [∵ CPCT]
∠BPA = ∠CPA [∵ CPCT]
∠BPA + ∠CPA = 180° [∵ Linear Pair]
⇒ ∠CPA + ∠CPA = 180° [∵ ∠BPA = ∠CPA]
⇒ 2∠ CPA = 180° ⇒ ∠CPA = (180°/2) = 90°
⇒ AP is perpendicular to BC. ⇒ AP is perpendicular bisector of BC. [∵ BP = CP].